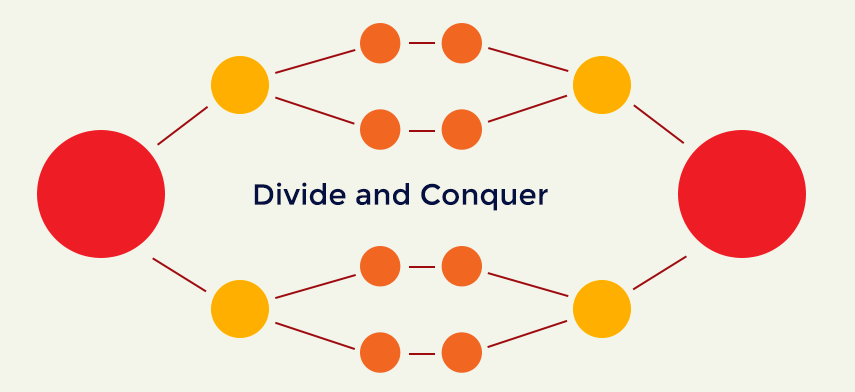
Giải thuật tham lam (greedy algorithm)

Công nghệ Lập trình Cấu trúc dữ liệu và giải thuật

Tham lam (hay tham ăn) là một trong những phương pháp phổ biến nhất để thiết kế giải thuật.

Nếu bạn đã đọc truyện dân gian thì sẽ có câu chuyện như thế này: trên một mâm cỗ có nhiều món ăn, món nào ngon nhất ta sẽ ăn trước, ăn hết món đó ta sẽ chuyển sang món ngon thứ hai, và chuyển tiếp sang món thứ ba…

Rất nhiều giải thuật nổi tiếng được thiết kế dựa trên ý tưởng tham lam, ví dụ như giải thuật cây khung nhỏ nhất của Dijkstra, giải thuật cây khung nhỏ nhất của Kruskal,…

Giải thuật tham lam (Greedy Algorithm) là giải thuật tối ưu hóa tổ hợp. Giải thuật tìm kiếm, lựa chọn giải pháp tối ưu địa phương ở mỗi bước với hi vọng tìm được giải pháp tối ưu toàn cục.

Giải thuật tham lam lựa chọn giải pháp nào được cho là tốt nhất ở thời điểm hiện tại và sau đó giải bài toán con nảy sinh từ việc thực hiện lựa chọn đó. Lựa chọn của giải thuật tham lam có thể phụ thuộc vào lựa chọn trước đó. Việc quyết định sớm và thay đổi hướng đi của giải thuật cùng với việc không bao giờ xét lại các quyết định cũ sẽ dẫn đến kết quả là giải thuật này không tối ưu để tìm giải pháp toàn cục.

Bạn theo dõi một bài toán đơn giản dưới đây để thấy cách thực hiện giải thuật tham lam và vì sao lại có thể nói rằng giải thuật này là không tối ưu.

Bài toán đếm số đồng tiền

Yêu cầu là hãy lựa chọn số lượng đồng tiền nhỏ nhất có thể sao cho tổng mệnh giá của các đồng tiền này bằng với một lượng tiền cho trước.

Nếu tiền đồng có các mệnh giá lần lượt là 1, 2, 5, và 10 xu và lượng tiền cho trước là 18 xu thì giải thuật tham lam thực hiện như sau:

Bước 1: Chọn đồng 10 xu, do đó sẽ còn 18 – 10 = 8 xu.

Bước 2: Chọn đồng 5 xu, do đó sẽ còn là 3 xu.

Bước 3: Chọn đồng 2 xu, còn lại là 1 xu.

Bước 4: Cuối cùng chọn đồng 1 xu và giải xong bài toán.

Bạn thấy rằng cách làm trên là khá ổn, và số lượng đồng tiền cần phải lựa chọn là 4 đồng tiền. Nhưng nếu chúng ta thay đổi bài toán trên một chút thì cũng hướng tiếp cận như trên có thể sẽ không đem lại cùng kết quả tối ưu.

Chẳng hạn, một hệ thống tiền tệ khác có các đồng tiền có mệnh giá lần lượt là 1, 7 và 10 xu và lượng tiền cho trước ở đây thay đổi thành 15 xu thì theo giải thuật tham lam thì số đồng tiền cần chọn sẽ nhiều hơn 4. Với giải thuật tham lam thì: 10 + 1 + 1 +1 + 1 + 1, vậy tổng cộng là 6 đồng tiền. Trong khi cùng bài toán như trên có thể được xử lý bằng việc chỉ chọn 3 đồng tiền (7 + 7 +1).

Do đó chúng ta có thể kết luận rằng, giải thuật tham lam tìm kiếm giải pháp tôi ưu ở mỗi bước nhưng lại có thể thất bại trong việc tìm ra giải pháp tối ưu toàn cục.