Giải thuật chia để trị (divide and conquer) là gì?
Phương pháp chia để trị (Divide and Conquer) là một phương pháp quan trọng trong việc thiết kế các giải thuật.
Ý tưởng của phương pháp này khá đơn giản và rất dễ hiểu: Khi cần giải quyết một bài toán, ta sẽ tiến hành chia bài toán đó thành các bài toán con nhỏ hơn. Tiếp tục chia cho đến khi các bài toán nhỏ này không thể chia thêm nữa, khi đó ta sẽ giải quyết các bài toán nhỏ nhất này và cuối cùng kết hợp giải pháp của tất cả các bài toán nhỏ để tìm ra giải pháp của bài toán ban đầu.
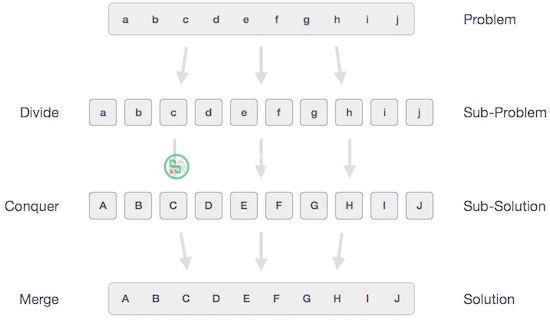
Nói chung, bạn có thể hiểu giải thuật chia để trị (Divide and Conquer) qua 3 tiến trình sau:
Tiến trình 1: Chia nhỏ (Divide/Break)
Trong bước này, chúng ta chia bài toán ban đầu thành các bài toán con. Mỗi bài toán con nên là một phần của bài toán ban đầu. Nói chung, bước này sử dụng phương pháp đệ qui để chia nhỏ các bài toán cho đến khi không thể chia thêm nữa. Khi đó, các bài toán con được gọi là "atomic – nguyên tử", nhưng chúng vẫn biểu diễn một phần nào đó của bài toán ban đầu.
Tiến trình 2: Giải bài toán con (Conquer/Solve)
Trong bước này, các bài toán con được giải.
Tiến trình 3: Kết hợp lời giải (Merge/Combine)
Sau khi các bài toán con đã được giải, trong bước này chúng ta sẽ kết hợp chúng một cách đệ qui để tìm ra giải pháp cho bài toán ban đầu.
Hạn chế của giải thuật chia để trị (Devide and Conquer)
Giải thuật chia để trị tồn tại hai hạn chế, đó là:
Làm thế nào để chia tách bài toán một cách hợp lý thành các bài toán con, bởi vì nếu các bài toán con được giải quyết bằng các thuật toán khác nhau thì sẽ rất phức tạp.
Việc kết hợp lời giải các bài toán con được thực hiện như thế nào.
Ta có thể viết một lược đồ đơn giản để miêu tả một giải thuật chia để trị như sau
// Giải bài toán A
DivideConquer (A) {
if (A đủ nhỏ) {
return Solve (A)
} else {
// Chia bài toán A thành các bài toán con: A1, A2, ... , An
for (i = 1; i <= n; i ++) {
// Gọi đệ quy để giải quyết từng bài toán con Ai
xi = DivideConquer (Ai)
}
// Kết hợp các nghiệm xi của các bài toán con Ai để nhận được nghiệm của bài toán A
combine(x1, x2, ..., xn)
}
}
Ví dụ giải thuật chia để trị
Dưới đây là một số giải thuật được xây dựng dựa trên phương pháp chia để trị (Divide and Conquer):
Merge Sort
Merge Sort là một thuật toán sắp xếp nổi tiếng, luôn có trong chương trình giảng dạy về Algorithms trên ghế nhà trường.
Mục tiêu của một thuật toán sắp xếp thì rất đơn giản, đó là sắp xếp lại một dãy số không có thứ tự, thành một dãy có thứ tự, từ nhỏ đến lớn (hoặc từ lớn đến nhỏ). Có rất nhiều thuật toán khác nhau để giải quyết vấn đề này. Các thuật toán đơn giản, và dễ hiểu, dùng đến 2 vòng lặp như Bubble Sort, Insertion Sort, Selection Sort thì đều cho độ phức tạp thuật toán trung bình là O(n2). Một số thuật toán hiệu quả hơn có thể cho độ phức tạp là O(nlogn). Và Merge Sort là một trong số đó.
Merge Sort cũng là một trong những ví dụ kinh điển về việc thiết kế giải thuật chia để trị. Ý tưởng cơ bản của Merge Sort như sau:
- Chia dãy số ra làm 2 nửa, nửa bên trái và nửa bên phải (bước Chia (Divide))
- Tiến hành sắp xếp 2 nửa (2 mảng) đó (bước Trị (Conquer)), bằng cách gọi đệ quy. Việc gọi đệ quy được dừng lại khi mảng con được chia ra chỉ còn có 1 phần tử. Lúc đó mảng ở vào trạng thái đã được sắp xếp rồi (do chỉ có 1 phần tử thôi mà
![😂]() )
)
- Sau khi có được 2 dãy con đã sắp xếp, thì ta dùng một thuật toán merge để tạo thành một dãy số mới được sắp xếp (Bước Tổng Hợp (Combine))
Thuật toán merge 2 dãy con đã được sắp xếp (giả sử là theo thứ tự từ nhỏ đến lớn), thành một dãy được sắp xếp có thể miêu tả như sau:
- Chạy vòng
whileduyệt hết các phần từ của mảng chứa nửa bên trái, ta gọi là mảngLvà mảng chứa nửa bên phải, ta gọi là mảngR - So sánh phần tử ở mảng
Lvới phần tử ở mảngR, phần tử nào nhỏ hơn, thì ta đưa vào mảng kết quả. Cứ như vậy cho đến khi duyệt hết số phần từ của một trong 2 mảng - Copy nốt số phần tử còn lại ở mảng còn lại vào mảng kết quả
Dưới đây là hình ảnh miêu tả một cách trực quan cách thức hoạt động của thuật toán merge sort.
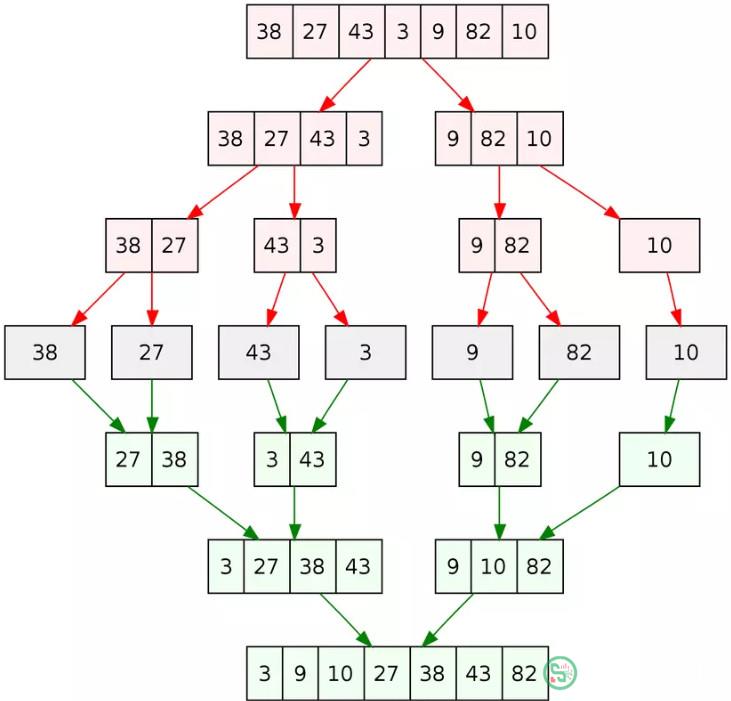
Còn dưới đây là một ví dụ về cách implementation của giải thuật Merge Sort
def mergeSort(A):
# Chỉ tiến hành sort khi số phần tử của mảng > 1. Hay nói cách khác, hàm đệ quy sẽ dừng lại khi chia thành mảng chỉ có một phần tử
# Lúc đó thì mảng đã ở trạng thái được sort sẵn rồi (do chỉ có 1 phần tử)
if len(A) > 1:
## Lấy phần tử ở giữa làm trung tâm
mid = len(A)//2
# Chia mảng ban đầu thành hai mảng L (left) và R (right)
L = A[:mid]
R = A[mid:]
# Gọi đệ quy để sort 2 mảng L và R
mergeSort(L)
mergeSort(R)
# Merge 2 mảng L và R đã được sắp xếp vào mảng kết quả
merge(A, L, R)
# Thuật toán để merge 2 mảng đã sắp xếp Left và Right thành 1 mảng được sắp xếp
def merge(A, L, R):
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
A[k] = L[i]
i += 1
else:
A[k] = R[j]
j += 1
k += 1
# Copy nốt các phần tử còn lại của mảng L hoặc mảng R vào mảng kết quả
while i < len(L):
A[k] = L[i]
i += 1
k += 1
while j < len(R):
A[k] = R[j]
j += 1
k += 1
if __name__ == '__main__':
A = [38, 27, 43, 3, 9, 82, 10]
mergeSort(A)
print(A)
Quick Sort
Quick Sort, hay sắp xếp nhanh, cũng là một trong những thuật toán nổi tiếng luôn được đề cập khi giảng dạy về Sorting Algorithm. Và nó cũng là một trong những ví dụ nổi tiếng cho việc thiết kế giải thuật chia để trị.
Trong khi Merge Sort chia danh sách cần sắp xếp thành hai danh sách con có kích thước tương đối bằng nhau nhờ chỉ số đứng giữa danh sách, thì Quick Sort lại chia danh sách cần sắp xếp thành hai danh sách con bằng cách so sánh từng phần tử của danh sách với một phần tử được chọn được gọi là pivot, hay phần tử chốt. Những phần tử nhỏ hơn hoặc bằng pivot được đưa về phía bên trái và nằm trong danh sách con thứ nhất, các phần tử lớn hơn chốt được đưa về phía bên phải và thuộc danh sách đứng sau. Cứ tiếp tục chia như vậy tới khi các danh sách con đều có độ dài bằng 1.
Cụ thể hơn, Quick Sort sử dụng cách thiết kế chia để trị với các bước như sau:
- Chọn phần tử pivot. Đây có thể là phần tử ở đầu, ở cuối, hoặc ở giữa của dãy số.
- Dùng 2 con trỏ chạy từ đầu dãy, và chạy từ cuối dãy. Với con trỏ chạy từ đầu dãy thì dừng lại khi gặp phần tử lớn hơn pivot. Với con trỏ chạy từ cuối dãy thì dừng lại khi gặp phần tử nhỏ hơn pivot. Swap 2 phần tử này với nhau và tiến hành duyệt tiếp. Dừng lại khi con trỏ chạy từ đầu gặp, hoặc vượt qua con trỏ chạy ngược lại từ cuối. Swap pivot vào vị trí hợp lý ta sẽ được 2 dãy con: 1 dãy gồm các phần tử nhỏ hơn pivot, 1 dãy gồm các phần tử lớn hơn pivot. Đây chính là 2 bài toán con mà ta cần tiếp tục giải quyết. Đến đây ta hoàn thành bước chia (divide)
- Gọi đệ quy để tiếp tục chia nhỏ các bài toán con ra, cho đến khi gặp bài toán con với độ dài là 1, tức ở trạng thái đã được sắp xếp rồi. Đến đây ta hoàn thành bước trị (conquer)
- Sau khi hoàn thành sắp xếp dãy bên trái nhỏ hơn pivot và dãy bên phải lớn hơn pivote, thì đơn giản ta chỉ cần ghép dãy bên trái, pivote, dãy bên phải về thành 1 mảng là có được kết quả cuối cùng là dãy được sắp xếp.
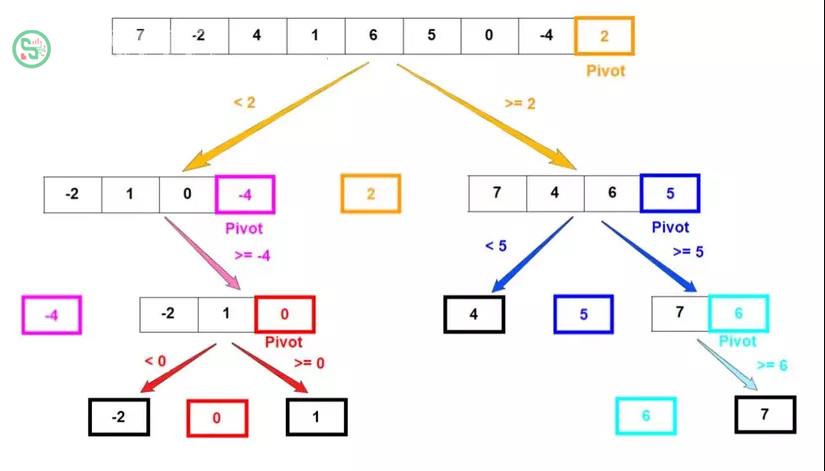
(Hình ảnh miêu tả cách thức Quick Sort hoạt động với cách chọn phần tử pivot ở cuối dãy)
Dưới đây là một ví dụ về cách implementation của giải thuật Quick Sort bằng Python
# Thuật toán để chia dãy số ra thành 2 phần, một phần nhỏ hơn phần tử pivot, một phần lớn hơn phần tử pivot
# phần tử pivot ở đây ta lấy là phần tử đầu tiên của mảng
def partition(start, end, A):
pivot_index = start
pivot = A[pivot_index]
# Chạy vòng lặp tăng dần con trỏ từ đầu dãy, là start, và giảm dần con trỏ từ cuối dãy, là end
# Dừng lại khi 2 con trỏ này gặp nhau
while start < end:
# Tăng dần con trỏ từ đầu dãy, cho đến khi gặp phần tử lớn hơn pivot
while start < len(A) and A[start] <= pivot:
start += 1
# Giảm dần con trỏ từ cuối dãy, cho đến khi gặp phần tử nhỏ hơn hoặc bằng pivot
while A[end] > pivot:
end -= 1
# Nếu khi có 2 phần tử này, mà start vẫn nhỏ hơn end thì swap chúng với nhau
# Mục tiêu là đưa hết phần tử nhỏ hơn hoặc bằng pivot sang một bên (bên trái)
# và đưa hết các phần tử lớn hơn pivot sang một bên (bên phải)
if(start < end):
A[start], A[end] = A[end], A[start]
# Khi vòng lặp bị break ra, thì phần tử end đang là phần tử nhỏ hơn pivot
# swap nó cho pivot ta sẽ đưa pivot về vị trí ngăn cách 2 dãy,
# một dãy bên trái gồm các phần tử nhỏ hơn, và dãy bên phải gồm các phần tử lớn hơn
A[end], A[pivot_index] = A[pivot_index], A[end]
# Trả về vị trí của pivot
return end
# Quick Sort mảng A, từ phần tử start đến phần tử end
def quick_sort(start, end, A):
# Chỉ tiếp tục chạy và gọi đệ quy khi mảng có hơn 1 phần từ (tức start < end)
if (start < end):
# Chia mảng A thành 2 phần,
# với vị trí p ngăn cách phần nhỏ hơn phần tử pivot, và phần lớn hơn phần tử pivot
p = partition(start, end, A)
# Gọi đệ quy để sắp xếp nửa bên trái và nửa bên phải
quick_sort(start, p - 1, A)
quick_sort(p + 1, end, A)
A = [38, 27, 43, 3, 9, 82, 10]
quick_sort(0, len(A) - 1, A)
print(A)
- Giải thuật tìm kiếm nhị phân (Binary Search)
- Nhân ma trận của Strassen
Chủ đề Tương tự
- Tags:
Không có đánh giá nào.
Viết một đánh giá.
Để bình luận vui lòng Đăng nhập tài khoản ! hoặcĐăng ký mới!

 )
)









 Ô tô, Xe máy
Ô tô, Xe máy Video
Video