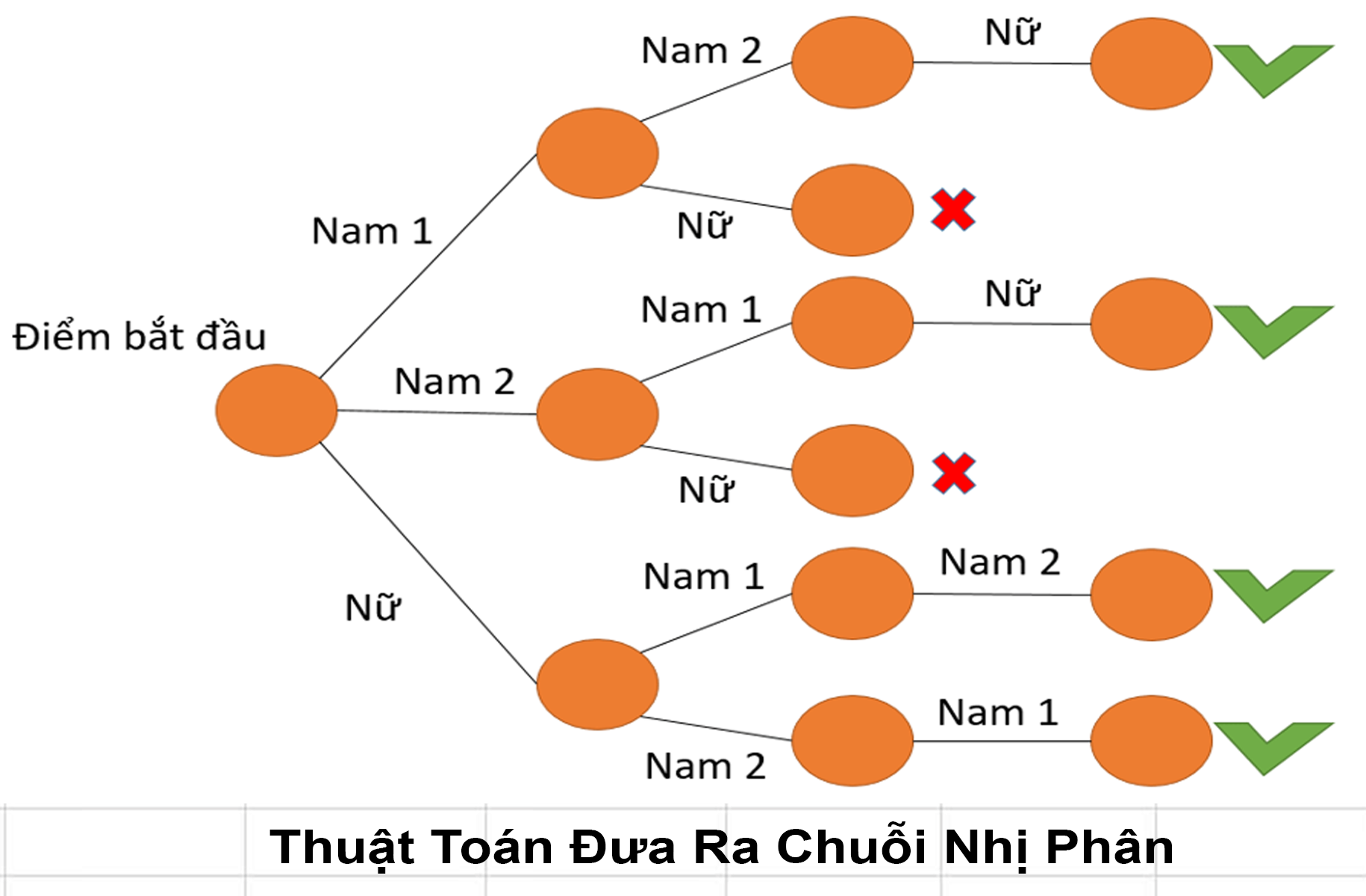
Thuật toán đưa ra chuỗi nhị phân

Công nghệ Lập trình Lập trình C++

26/12
Hai Tao
Lập trình C++
0
504

Hệ nhị phân (hay hệ đếm cơ số hai hoặc mã nhị phân) là một hệ đếm dùng hai ký tự để biểu đạt một giá trị số, bằng tổng số các lũy thừa của 2

1. Chuỗi nhị phân là gì?

1.1 Khái niệm về chuỗi nhị phân

Hệ nhị phân (hay hệ đếm cơ số hai hoặc mã nhị phân) là một hệ đếm dùng hai ký tự để biểu đạt một giá trị số, bằng tổng số các lũy thừa của 2. Hai ký tự đó thường là 0 và 1, chúng thường được dùng để biểu đạt hai giá trị hiệu điện thế tương ứng (có hiệu điện thế, hoặc hiệu điện thế cao là 1 và không có, hoặc thấp là 0). Do có ưu điểm tính toán đơn giản, dễ dàng thực hiện về mặt vật lý, chẳng hạn như trên các mạch điện tử, hệ nhị phân trở thành một phần kiến tạo căn bản trong các máy tính đương thời.

Ví dụ 0, 1, 0000, 0001, 010101, 00011100 là các chuỗi nhị phân

1.2 Bài toán đưa ra chuỗi nhị phân độ dài N

Chắc hẳn ai học về giải thuật cũng đã từng nghe qua và làm về bài toán đưa ra chuỗi nhị phân độ dài N rồi, nếu bạn mới bắt đầu học hoặc đã bỏ lỡ qua bài toán thú vị này thì cũng đừng lo, vì ngay bây giờ mình sẽ giới thiệu về nó nhé.

Bài toán cụ thể như sau:

Nhập vào một số nguyên dương N (1 ≤ N ≤ 20) hãy đưa ra tất cả các chuỗi nhị phân độ dài N, một chuỗi ghi trên một dòng, các chuỗi được sắp xếp từ bé đến lớn theo thứ tự từ điển,

Ví dụ 1:

Input

Output

Ví dụ 2:

Input

Output

Ví dụ 3:

Input

Output

000

001

010

011

100

101

110

111

Bài toán khá là thú vị đúng không nào, đã có ai có ý tưởng làm bài này chưa? hãy thử làm nó nhé, nếu bạn đã làm xong hoặc chưa biết làm thì cũng xem thử mình đã xử lý bài toán này bằng cách nào nhé.

2. Một số thuật toán đưa ra chuỗi nhị phân độ dài N

2.1 Biến đổi số thành chuỗi nhị phân

Thực chất các chuỗi nhị phân độ dài N lần lượt là biểu diễn nhị phân của các số thập phân từ 0 đến 2^N-1.

Ví dụ 0 = 0₍₂₎, 1 = 1₍₂₎, 2 = 10₍₂₎, 7 = 111₍₂₎.

Việc cần làm của chúng ta rất đơn giản đó là chỉ cần chuyển đổi các số tự nhiên từ 0 đến 2^N-1 sang chuỗi nhị phân là được (chú ý nhớ chèn các ký tự '0' vào các chuỗi nhị phân để độ dài của chuỗi nhị phân đủ N).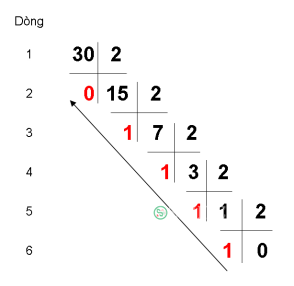

Để chuyển một số tự nhiên sang chuỗi nhị phân ta có thể làm như sau:

string decToBin(int n){
    string ans = "";
    while (n > 0) {
        ans = char (n % 2 + '0') + ans;
        n /= 2;
    }
    while (ans.length() < N)
        ans = "0" + ans;
    return ans;
}

Ta sẽ chia N cho 2 cho đến khi kết quả bằng 0, mỗi lần chia như vậy ta lưu lại số dư của N cho 2, chuỗi nhị phân của N chính là chuỗ số dư được đọc ngược.

CODE:

#include <iostream>
#include <math.h>
 
using namespace std;
 
int N;
 
string decToBin(int n){
    string ans = "";
    while (n > 0) {
        ans = char (n % 2 + '0') + ans;
        n /= 2;
    }
    while (ans.length() < N)
        ans = "0" + ans;
    return ans;
}
 
int main(){
    cin >> N;
    int N_2 = pow(2, N);
    for (int i = 0; i < N_2; i++)
        cout << decToBin(i) << endl;
}

2.2 Đệ quy quay lui

Với bài này ta có thể dùng phương pháp đệ quy, hiểu đơn giản là chúng ta cần dùng N vòng for lồng nhau, mỗi vòng for biến chạy sẽ chạy từ 0 đến 1.

phương pháp này để các bạn luyện tập đệ quy rất tốt, nhưng mình không khuyến khích các bạn dùng đệ quy trong khi nó có thể làm theo cách khác nha.

CODE:

#include <iostream>
 
using namespace std;
 
int N;
 
int x[100];
 
void in(int x[]){
    for (int i = 1; i <= N; i++)
        cout << x[i];
    cout << endl;
}
 
void deQuy(int i){
    for (int j = 0; j <= 1; j++){
        x[i] = j;
        if (i == N)
            in(x);
        else
            deQuy(i + 1);
        
    }
}
 
int main(){
    cin >> N;
    deQuy(1);
}

2.3 Phương pháp sinh

Ta thấy rằng nếu lấy lần lượt các chuỗi nhị phân độ dài N - 1, sau đó thêm ký tự 0 hoặc 1 vào cuối chuỗi đó, ta sẽ được 2 chuỗi nhị phân độ dài N.

Ví dụ như các chuỗi nhị phân độ dài 2 có các chuỗi là "00", "01", "10", "11".

Với chuỗi "00" khi ta thêm vào cuối nó ký tự '0' hoặc '1' ta có chuỗi "000" và "001".

Tương tự với chuỗi "01" ta sẽ có chuỗi "010" và "011".

Tương tự với chuỗi "10" ta sẽ có chuỗi "100" và "101".

Tương tự với chuỗi "11" ta sẽ có chuỗi "110" và "111".

Như vậy chỉ cần 2 ký tự "0" và "1" ta có thể sinh ra các chuỗi nhị phân độ dài N.

CODE:

#include <iostream>
#include <math.h>
 
using namespace std;
 
int N;
 
string a[100009];
 
int main(){
    cin >> N;
    int n = 2;
    a[0] = "0";
    a[1] = "1";
    int k = 0;
    while (a[k].length() < N){
        a[n++] = a[k] + "0";
        a[n++] = a[k] + "1";
        k++;
    }
    for (int i = k; i < n; i++)
        cout << a[i] << endl;
}

2.4 Tìm chuỗi nhị phân tiếp theo

Với phương pháp này ta sẽ tìm chuỗi nhị phân tiếp theo khi biết được chuỗi nhị phân trước đó, ví dụ tiếp theo của chuỗi "101" là "110", tiếp theo của "111" là "1000", vậy là sao làm được như vậy.

Cách làm sẽ là với chuỗi nhị phân S, để tìm chuỗi nhị phân tiếp theo của S ta sẽ làm như sau.

- Tìm vị trí index là vị trí của bit khác '0' cuối cùng của S.

- Thay thì bit thứ index từ '0' thành '1'.

- Biến đổi tất cả bit '1' thành '0' từ vì trí index + 1 đến hết chuỗi.

Ví dụ:

Với chuỗi S = "10011", thì ta có bit bằng '0' cuối cùng là bit thứ 3, ta biến đổi bit 3 thành 1 và bit 4, bit 5 thành 0, ta sẽ được chuỗi nhị phân tiếp theo của S là "10100".

CODE:

#include <iostream>
#include <math.h>
 
using namespace std;
 
int N;
 
string next(string s){
    for (int i = s.length() - 1; i >= 0; i--)
        if (s[i] == '0'){
            s[i] = '1';
            return s;
        } else
            s[i] = '0';
    return "";
}
 
int main(){
    cin >> N;
    string s = "";
    for (int i = 0; i < N; i++)
        s = "0" + s;
    for (int i = 0; i < pow(2, N); i++){
        cout << s << endl;
        s = next(s);
    }
}